
二叉查找树
前序、中序、后续、层序遍历
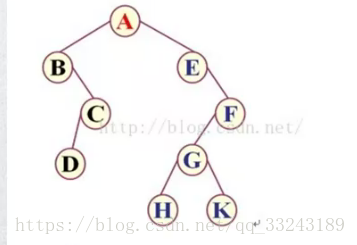
- 前序遍历:ABCDEFGHK
- 中序遍历:BDCAEHGKF
- 后序遍历:DCBHKGFEA
- 层序遍历:ABECFDGHK
哈夫曼树
树的带权路径最小的二叉树叫做哈夫曼树或最优二叉树
例如某二叉树有4个叶子结点a、b、c、d,分别带权7、5、2、4,从根节点到叶子结点的路径都为2,则它们的带权路径长度为
WPL = 7*2 + 5*2 + 2*2 + 4*2 = 36
如何创建?
从所有的节点中选出两个权值最小的组成一个新的节点A,A与剩余节点再重复上述步骤直到节点使用完。
哈夫曼编码
我们约定左分支表示字符’0’,右分支表示字符’1’,在哈夫曼树中从根结点开始,到叶子结点的路径上分支字符组成的字符串为该叶子结点的哈夫曼编码
AVL树
二叉查找树有可能完全退化成了线性结构,即所有节点都是左节点或者右节点。
平衡树通过旋转来保持平衡,而旋转是非常耗时的,由此我们可以知道AVL树适合用于插入删除次数比较少,但查找多的情况。
- 其是二叉查找树并满足二叉查找树性质
- 任何节点的左右子节点高度差不能够大于1
红黑树
红黑树是一种弱平衡二叉树
确保没有一条路径会比其它路径长出两倍
相对于要求严格的AVL树来说,它的旋转次数变少,所以对于搜索,插入,删除操作多的情况下,我们就用红黑树.
特点如下:
- 节点非黑即白
- 根节点一定是黑色
- 每个叶子节点都是黑色的空节点
- 每个红色节点下的子节点必须为黑色
- 从任意节点到其每个叶子节点的所有路径都包含相同的黑色节点
在插入后先执行变色,变色到一定程度后无法解决问题再执行旋转
旋转包括左旋转、右旋转
B树
- 与红黑树相比,在相同的的节点的情况下,一颗B/B+树的高度远远小于红黑树的高度
- B/B+树上操作的时间通常由I/O时间和CPU计算时间构成
- CPU的速度非常快,所以B树的操作效率取决于访问磁盘的次数
- 节点存放有key、下一个节点的指针、value
B+树
- 应文件系统所需而产生的一种B树的变形树
- 非叶子节点只保存索引,不保存实际的数据
- 数据都保存在叶子节点中
- 叶子结点中的实际数据通过链表链接在一起,使得遍历整棵树之要遍历叶子结点就行
B+树相对B树的优势
- B树的操作效率主要由IO读写次数影响,而由于B+树非叶子结点不存放数据只存放key,那么导致一次io可以从内存中操作更多的节点,因此效率高于b树。
- 由于只是叶子结点存放内容。那么从根节点查询关键字的路径长度相同,导致每一个数据的查询效率相当
版权声明:本文为博主原创文章,欢迎转载,转载请注明作者、原文超链接,感谢各位看官!!!
本文出自:monkeyGeek
座右铭:生于忧患,死于安乐
欢迎志同道合的朋友一起交流、探讨!
 monkeyGeek
monkeyGeek

