
前言
Google Chubby的作者Mike Burrows说过这个世界上只有一种一致性算法,那就是Paxos,其它的算法都是残次品。
Paxos算法问世已经有将近30年的历史了,是目前公认最有效的解决分布式场景下一致性问题的算法之一,但是缺点是比较难懂,工程化比较难。
Paxos算法是用来解决分布式系统中,如何就某个值达成一致的算法。
一致性问题
什么是一致性问题?
假设有一组服务器保存了用户的余额,初始是100块,现在用户提交了两个订单,一个订单是消费10元,一个订单是充值50元。由于网络错误和延迟等原因,导致一部分服务器只收到了第一个订单(余额更新为90元),一部分服务器只收到了第二个订单(余额更新为150元),还有一部分服务器两个订单都接收到了(余额更新为140元),这三者无法就最终余额达成一致。这就是一致性问题。
一致性问题的传统解法?
当集群环境存在一致性问题时我们最容易想到的是建立一个”协调者”,通过协调者来保证一致性.但是如果协调者宕机了呢?
如果协调者宕机我们可能回想到建立协调者集群,这时又出现协调者间的一致性问题….
Paxos是能够基于一大堆完全不可靠的网络条件下却能可靠确定地实现共识一致性的算法。也就是说:它允许一组不一定可靠的处理器(服务器)在某些条件得到满足情况下就能达成确定的安全的共识,如果条件不能满足也确保这组处理器(服务器)保持一致。
需要注意的是paxos的应用场景是假定各消息提供方提供的消息是真实有效的,伪造消息不在paxos研究范围内,Byzantine Paxos 以及区块链技术是paxos的升级和应用,能够有效避免伪造消息等情况发生.
paxos的发展历史及演变
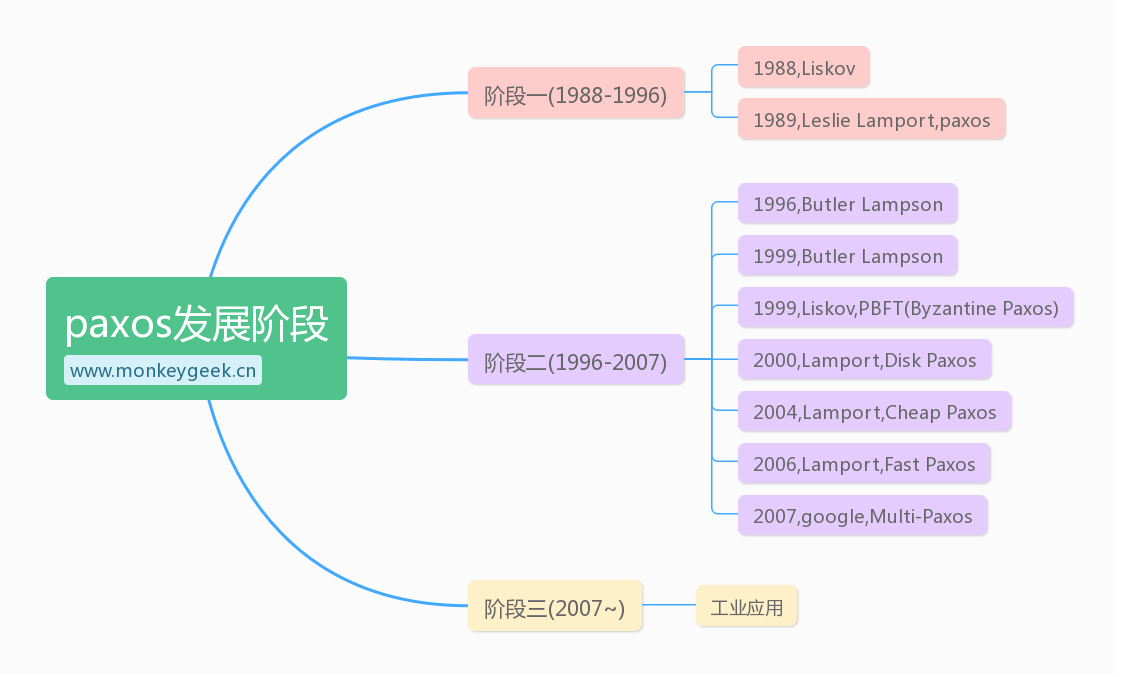
从上图可以看出paxos发展分为三个阶段:
- 1988年Lislov(利斯洛夫)等人在PODC(分布式计算原理学术讨论会)上发表了一篇文章,关于副本宕机,分布式系统仍能够正常运行的算法,该算法本质上与Paxos一致
- 1989年Leslie Lamport在1989年提出Paxos这个名称,但他的论文因为过于艰涩,未能发表。
- 1996年,Lamport论文的正式发表(与8年前第一次投稿相比,几乎未改)。
- 1999年,Butler Lampson等人重新描述和证明了Paxos算法,并分析了其时间开销及容错性。
- 1999年,Liskov等人提出了PBFT(实用的拜占庭容错算法)被Lampson称为Byzantine Paxos,该算法对基础Paxos进行了改进,使其可以处理拜占庭错误。
- 2000年,Lamport在提出了Disk Paxos,这可以认为是Paxos基于磁盘的版本,以支持持久化。
- 2004年,Lamport提出了Cheap Paxos,其提升了算法的容错性
- 2006年,Lamport提出了Fast Paxos,其降低了消息延迟
- 2007年,google公司研究小组提出了Multi-Paxos,其将paxos中的论证阶段进行简化,提高了效率
- 2007年及其以后google公司在OSDI发表的两篇论文拉开了paxos工业应用的序幕
Paxos算法流程
Paxos中的角色
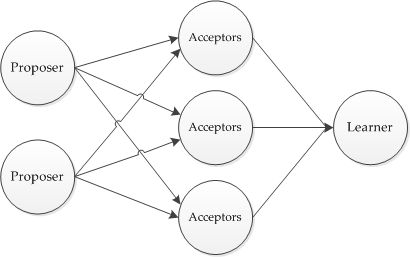
- Proposer(提议人):负责提出提案(Proposal),Proposal信息包括提案编号 (Proposal ID) 和提议的值 (Value)
- Acceptor(接收人):参与决策,回应Proposers的提案
- Learner(学习者):不参与决策,从Proposers/Acceptors学习最新达成一致的提案(Value)
注:在多副本状态机中,每个副本同时具有Proposer、Acceptor、Learner三种角色
Paxos的决议阶段
- 第一阶段:Prepare阶段。Proposer向Acceptors发出Prepare请求,Acceptors针对收到的Prepare请求进行Promise承诺。
- 第二阶段:Accept阶段。Proposer收到多数Acceptors承诺的Promise后,向Acceptors发出Propose请求,Acceptors针对收到的Propose请求进行Accept处理。
注:在第二阶段结束后如果Proposer收到多数Acceptors的Accept,标志着本次Accept成功,决议形成,将形成的决议发送给所有Learners
Acceptor的两个承诺一个应答
两个承诺(可重复接受)
- 不再接受Proposal ID小于等于(注意:这里是<= )当前请求的Prepare请求。
- 不再接受Proposal ID小于(注意:这里是< )当前请求的Propose请求。
一个应答
- 不违背以前作出的承诺下,回复已经Accept过的提案中Proposal ID最大的那个提案的Value和Proposal ID,没有则返回空值。
Paxos算法伪代码Base-Paxos
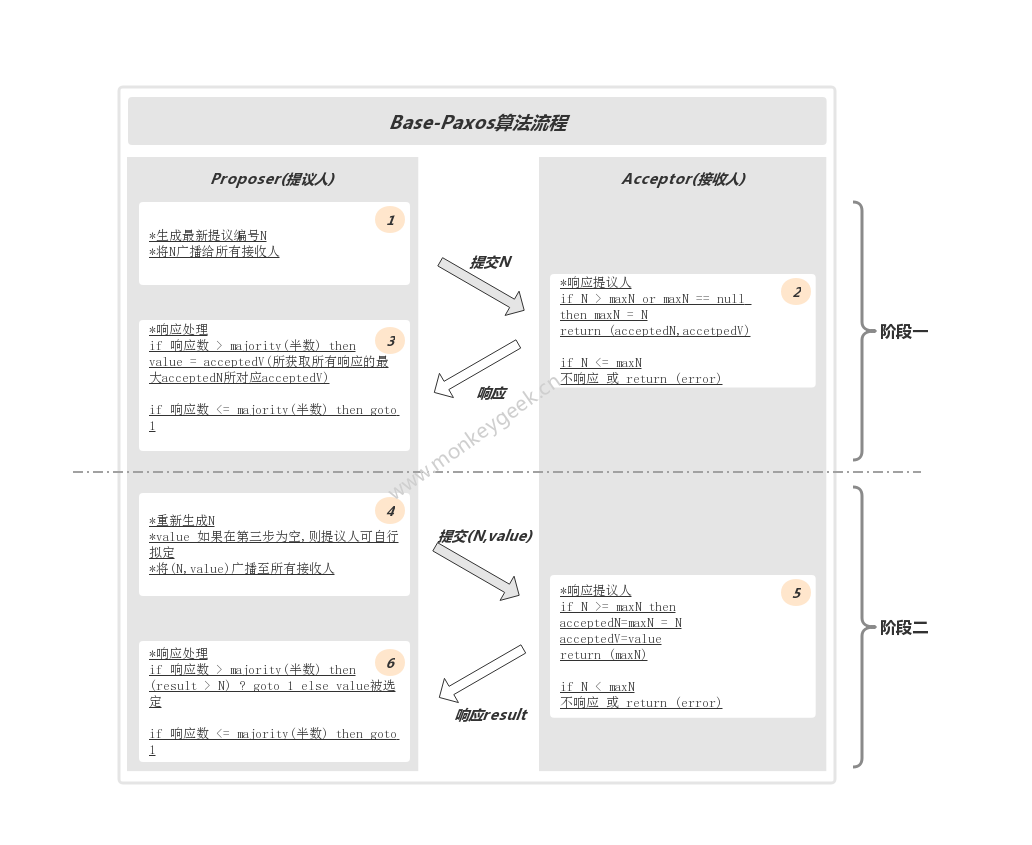
- 步骤1:提议人生成最新提议编号N(N自增且唯一,Paxos不同实现其N的生成算法不同),并将N广播至所有接收人
- 步骤2:接收人响应提议人Proposal,如果接收人maxN(记录最大N)为null则记录N到maxN并返回(null,null),如果N>maxN则记录N到maxN并返回(acceptN,accetpV),如果N<=maxN则不响应
- 步骤3:提议人收集所有来自接收人的响应数据,如果响应数量小于等于半数则重新执行步骤1,否则将从所获取所有响应的最大编号accetpedN所对应的acceptedV作为阶段二value的提交值.
- 步骤4:此步骤提议人将提交(N,value)至所有接收人,其中N将重新生成,value来自步骤3,如果value==null则将有提议人自行决定
- 步骤5:接收人将针对提议人的(N,value)进行响应,如果N小于maxN,接收人不响应,否则,接收人将更新maxN,accetpedN,accetpedV并返回(acceptN,accetpV)
- 步骤6:由提议人根据响应结果确定value的决议结果并将结果分发至各Learner,其中如果响应数过半数但响应结果的编号result大于发送编号N,那么证明value有被更新,需要重新执行步骤1
总结:
- 阶段一本质上是收集各接收人现存(acceptN,accetpV)并为阶段二的数据提交做准备
- 阶段二本质上是完成决议确定value值并将决议结果发送至各Learner
注:原始的Paxos算法(Basic Paxos)只能对一个值形成决议,决议的形成至少需要两次网络来回,在高并发情况下可能需要更多的网络来回。如果想连续确定多个值,Basic Paxos搞不定了。因此Basic Paxos几乎只是用来做理论研究,并不直接应用在实际工程中。
Paxos算法推导
算法目标
- T1.一次选举必须要选定一个议案(不能出现所有议案都被拒绝的情况)
- T2.一次选举必须只选定一个议案(不能出现两个议案有不同的值,却都被选定的情况)
约束条件
P0.:当集群中,超过半数的Acceptor接受了一个议案,那我们就可以说这个议案被选定了(Chosen)
P0已经是一个完备的一致性算法,保证了P0也就解决了一致性问题。但是P0的实用性不佳,一个议案想被半数以上的Acceptor接受是一件极其困难的事情!
P1:Acceptor必须接受(Accept)它所收到的第一个Proposal
为什么必须满足P1,我们设想一个极端场景,比如环境中只存在一个Proposal和一个Acceptor,当Proposal发送的提案由于特殊原因被acceptor拒绝,那么这时违反了T1,即T1的隐含条件包含了P1
P2:如果一个值为v的议案被选定了,那么被选定的更大编号的议案,它的值必须也是v
- P2-1:假设v1被选定,由P0可知议案被选定必定有超过半数的Acceptor接受v1
- P2-2:同理少于半数的Acceptor可能接受了不同的v2,v3,vx……(为什么少于半数的Acceptor会接受非v1,原因可能是多样的,例如由P1造成,或者网络发送不及时等.)
- P2-3:由P2-1与P2-2我们知道在整个集群环境下v1是超过半数的,理应被选中的,但是实际环境常常不如人意,例如由于网络问题v1并没有及时的通知到各Proposer,那么有可能产生v2或者v3被认为是超过半数的从而被选定,这是有多个议案被选定显然是违背了T2的.
- P2-4:如果存在多个v1,v2,v3被选定那么只需要保证v1=v2=v3也可以满足T1.那么如何满足多个被选定值相等呢?
- P2-5:如果要满足多个选定值相等只需满足”其它的”编号也同为v1(假设为集合A)或者”更大的”编号也为v1(假设为集合B)即可,显然B∈A,我们只需要满足B即可
- P2-6:我们知道Acceptor的”两个承诺,一个应答”决定了Accetpor只会接受编号大于当前编号的提案,只需满足最大编号对应的v也是v1即可满足多个被选定值相同从而满足T1.以上即为P2存在的意义.
总结:
如果P1和P2都被满足那么Paxos的目标T1和T2就能够实现,想要确保P1成立很简单,但是想要使P2成立必须要继续添加约束条件.
P2a:如果一个值为v的议案被选定了,那么Acceptor接受的更大编号的议案,它的值必须也是v
P2a是P2的充分条件,即Acceptor接受议案是Proposer选定议案的前提.所以只需满足P2a即可满足P2,但是想要满足P2a并不容易,例如已经选定v1(超过半数),但是由于网络原因之前的Proposer广播v1时并没有送达某Acceptor(假设a1),这个时候如果a1从未接受过提议,那么根据P1,a1必须接受其它Proposer的提议内容v2,此时v1!=v2这违背了P2a.因此需要P2b来进行进一步约束.
P2b:如果一个值为v的议案被选定了,那么Proposer提出的更大编号的议案,它的值必须也是v
P2b是P2a的充分条件,即Proposer的提议是Acceptor接受的前提条件.想要满足P2b也不容易,受网络环境影响,例如提议人a(简称Pa)在12:02:20 50时间点发送提议(N1,V1),当在12:02:20 59时提议全部送达所有Acceptor,此时接收人超过半数V1被选定.但是由于网络原因Pb在12:02:20 55时发现当前环境并没有被选中的提案因此提议(N2,V2),这时将违反P2b,需要P2c对其进行进一步约束.
P2c:在所有Acceptor中,任意选取半数以上的Acceptor集合,我们称这个集合为S。Proposal新提出的议案(简称Pnew)必须符合下面两个条件之一
P2c-1:如果S中所有Acceptor都没有接受过议案的话,那么Pnew的编号保证唯一性和递增即可,Pnew的值可以是任意值
P2c-2:如果S中有一个或多个Acceptor曾经接受过议案的话,要先找出其中编号最大的那个议案,假设它的编号为N,值为V。那么Pnew的编号必须大于N,Pnew的值必须等于V
P2c有效性证明
实现了P2c就可以满足P2b进而最终实现Paxos目标,但是如何证明P2c是能够满足P2b的呢?以下内容为作者通过数学归纳法的证明:
题目:已知议案 $(m, v_a)$,是集合中第一个被选定的议案,接受这个议案的Acceptor集合为 **$S_m$**,在满足P2c的规则2的情况下,提出了一个新的议案 $(n, v_b)$,其中$n>m$,证明$v_b = v_a$
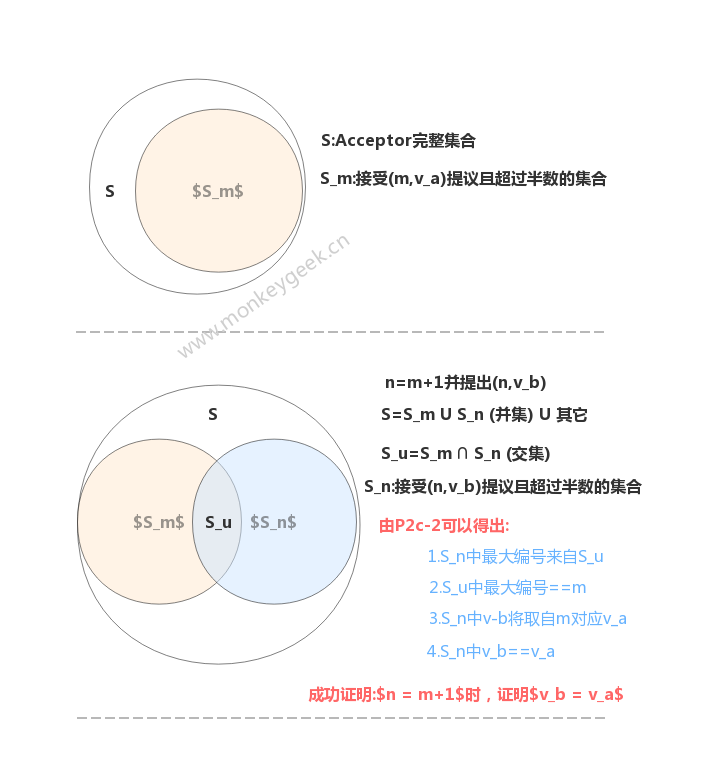
步骤一:当议案的编号$n = m+1$时,证明$v_b = v_a$
因为$(m, v_a)$是第一个被选定的议案,因此在$m+1$提出之前,$m$必然是集群当中编号最大的议案。
根据P2c的规则2,议案$(m+1,v_b)$能够被提出,是因为存在一个多数派集合$S_n$,这个集合中,编号最大的议案的值为$v_b$。因为$Sm$和$Sn$都是多数派集合,所以他们必定存在交集。交集中的Acceptor必定都接受了$(m,v_a)$,$m$是整个集群最大的编号,当然也是$S_n$中最大的编号,根据P2c的规则2,议案$m+1$的值只能是$v_a$,若$v_b$不等于$v_a$,将导致矛盾,因此$v_b = v_a$

步骤二:当$n > m+1$时,假设编号从$m+1$到$n-1$的议案的值都是$v_a$,证明$v_b = v_a$
编号为$m+1$到$n-1$的议案提出后,我们没办法判断究竟那一个议案会被选定,但有一点是可以肯定的:所有接受了$v_a$的Acceptor构成了一个新的集合$S_{n-1}$,这个集合包含了集合$Sm$中的所有Acceptor,$S_{n-1}$显然是一个多数派集合,这个集合接受的议案的编号在$m$到$n-1$之间,而且值为$v_a$。没有包含在集合$S_{n-1}$中的Acceptor所接受的议案一定小于$m$。
根据P2c的规则2,议案$(n,v_b)$能够被提出,那么一定存在一个多数派集合$Sn$,$Sn$中接受的最大编号的议案的值为$v_b$。因为$S_n$和都$S_{n-1}$是多数派集合,所以他们必定存在交集。交集中的议案的最大编号一定在$m$到$n-1$之间。因此$S_n$集合中编号最大的议案一定位于交集内。根据P2c的规则,此时$v_b$必定等于$v_a$。
编号的生成规则
编号用来区分不同的议案,每一个Proposer在提交议案时必须生成编号,编号必须具备如下性质:
- 唯一性
- 递增性
编号的生成算法有多种,在《Paxos made simple》中提到,推荐Proposer从不相交的数据集合中进行选择.
方案一:
假设有n个proposer,每个编号为ir(0<=ir<n),proposal编号的任何值s都应该大于它已知的最大值
s = m * n + i (其中s表示本次编号生成结果,m表示生成次数,n表示proposer数量,i表示下标)
这样即可确保不相交集合.
例如:第一次提交时各proposer的编号生成如下:(假设有三个proposer)
P1=1*3+0=3
P2=1*3+1=4
P3=1*3+2=5
……
方案二:
在实践过程中,可以用 时间戳 + 提出提案的次数 + 机器 IP/机器ID 来保证唯一性和递增性。
活锁的产生
活锁的产生原因本质上是多个proposer均认为自己提交的编号过低,从而生成最新的递增版本号重复提交,这样会导致死循环,新轮次的抢占会使旧轮次停止运行,如果每一轮在第二阶段执行成功之前 都 被 新一轮抢占,这种情况被称为活锁.活锁的产生原因多种多样,可能是网络原因等造成.
这个问题在实际应用会发生地比较少,一般可通过 随机改变 ProposalID的增长幅度 或者 增加Proposer发送新一轮提案的间隔 来解决。
参考文献如下:
https://blog.csdn.net/cnh294141800/article/details/53768464
https://www.cnblogs.com/stateis0/p/9062130.html
https://blog.csdn.net/yowasa/article/details/81224936
https://blog.csdn.net/omnispace/article/details/79653932
https://zhuanlan.zhihu.com/p/43800991
https://zhuanlan.zhihu.com/p/69817030
版权声明:本文为博主原创文章,欢迎转载,转载请注明作者、原文超链接,感谢各位看官!!!
本文出自:monkeyGeek
座右铭:生于忧患,死于安乐
欢迎志同道合的朋友一起交流、探讨!
 monkeyGeek
monkeyGeek


